In the tech startup ecosystem, the term "exponential growth" is frequently used to describe a company’s rapid early-stage expansion. However, this description often fails to capture the true nature of long-term growth trajectories. From an econometric standpoint, what is commonly referred to as exponential growth is, in many cases, more accurately characterized by a sigmoidal curve, constrained by fundamental market forces such as total addressable market (TAM) and market saturation. This article explores the econometric principles behind startup growth and explains why the sigmoidal model provides a more accurate reflection of the typical startup lifecycle.
1. Exponential growth: the early illusion
At the inception of a high-growth startup, revenue or user base typically exhibits a rapid acceleration, reminiscent of an exponential function:
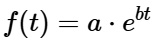
where a is the initial size, b is the growth rate, and t is time. The defining characteristic of exponential growth is its constant growth rate, implying that, theoretically, it continues indefinitely without any structural impediments.
For early-stage companies, the rapid uptake of a product can simulate this behavior, especially when network effects and first-mover advantages are in play. However, this growth model assumes no external constraints, a major simplification that fails to consider the realities of market saturation.
2. Sigmoidal growth: A more accurate representation
In contrast, a more appropriate model for long-term growth is the sigmoid function, often expressed as the logistic growth function:
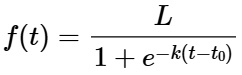
where:
- L represents the upper bound (asymptote), which can be interpreted as the maximum market share a startup can achieve within a given total addressable market.
- k is the growth rate.
- t⁰ is the inflection point, where growth is most rapid.
The sigmoidal growth model acknowledges the presence of a ceiling, accounting for constraints such as market size, competition, and diminishing returns on new customer acquisition. Initially, growth resembles an exponential curve, but over time, it decelerates as the startup approaches its market saturation point.
3. Econometric interpretation of growth dynamics
From an econometric perspective, the startup growth process can be seen as evolving through three distinct phases, which correspond to different sections of the sigmoidal curve:
- Phase 1: Initial acceleration (exponential growth phase)
Early in a startup’s lifecycle, marginal returns to scale are high. The customer acquisition cost is relatively low, and the market is far from saturated, leading to a period of apparent exponential growth. This phase can be modeled econometrically using time-series data that exhibits positive autocorrelation in growth rates.
- Phase 2: Inflection point (rapid growth deceleration)
As the startup scales, market dynamics change. Increased competition, rising customer acquisition costs, and saturation of early adopter segments lead to a diminishing marginal growth rate. Econometric models begin to show structural breaks in the data as growth decelerates, often necessitating the transition from exponential to logistic (sigmoidal) modeling techniques. Techniques such as non-linear regression or logistic time-series models become more appropriate at this stage.
- Phase 3: Saturation (asymptotic phase)
In the long-run, growth approaches an asymptote where the firm's market share stabilizes at or near its maximum possible penetration. The growth rate approaches zero as the law of diminishing returns fully takes effect. In econometric terms, this phase reflects convergence toward an equilibrium, often modeled using stochastic differential equations with long-term constraints.
4. Empirical validation of sigmoidal growth in startups
- In early-stage startups, user base growth often follows a power law, where network effects drive rapid adoption. However, as the company matures and begins to saturate its market, growth slows significantly, indicating the need to transition from an exponential model to a logistic model.
- A typical case can be observed in the scaling trajectory of social media platforms. Initially, they exhibit strong network effects, leading to exponential user growth. Over time, however, user acquisition plateaus as the platform saturates its addressable market. Empirical data for platforms like Facebook or Instagram shows a clear sigmoidal curve when modeling monthly active users over time.
Econometric models that fail to account for the sigmoidal nature of growth will overestimate future growth rates and misprice startup valuations, particularly during later stages of the startup lifecycle.
5. Implications for startup valuation and strategy
Understanding the sigmoidal nature of startup growth has critical implications for both investors and founders:
- Valuation models
Traditional discounted cash flow (DCF) models, which assume constant exponential growth, may grossly overvalue startups. In contrast, models incorporating a logistic growth function provide a more realistic long-term forecast by accounting for eventual market saturation.
- Strategic decisions
For founders, recognizing the sigmoidal curve implies the importance of identifying the inflection point early and shifting focus from hyper-growth strategies (focused on rapid user acquisition) to sustained growth strategies (focused on increasing customer lifetime value, improving margins, or expanding into adjacent markets).
The narrative of exponential growth in the startup ecosystem is compelling but ultimately incomplete. In the long run, growth is almost always constrained by fundamental economic forces, leading to sigmoidal behavior. Recognizing this dynamic is crucial for econometric modeling, strategic decision-making, and valuation. For startups and investors alike, understanding the real shape of growth is the key to sustainable success.
René Vergara-Fuentes
René is a co-founder, CEO and Head of Technology at Factorial Biomechanics.